22/5/19 円柱の公式(計算式) 円柱の体積V V = π r 2 h 円柱の表面積S S = 2 π r r h 円柱の側面積F F = 2 π r h円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。 側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので、上下の円の面積を求め11/4/15 まとめ:円柱の体積の求め方は楽勝すぎる! 円柱の体積の求め方はどうだったかな?? 半径×半径×円周率×高さ で円柱の体積は計算できたね。 円柱の体積を計算できるようになったらついでに円柱の表面積の求め方にもチャレンジしてみよう!

円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト
円柱の面積の求め方
円柱の面積の求め方-円柱の表面積 V = 2πr2 2πrh V = 2 π r 2 2 π r h 表面積 = 2 × 半径 × 半径 × 314 直径 × 314 × 高さ 公式の導出方法と計算例については、「 円柱の表面積の求め方 」をご覧ください。12/3/ 面積を求める例題 まずは面積を求める例題から説明します。面積を求めるときのポイントは どのような線が集まって面を形成しているか をイメージすることが大切です。 三角形 下の図のように\(y=x\)の直線があり、原点,\((1,0)\),\((1,1)\)の3点を結ぶ三角形の面積\(S\)を求めてみたいと思



立体の体積と表面積 1 柱体の表面積
のどこの面積が求められるか 考える。 ・ 四角柱の体積の求め方をまと める。 ・直方体,立方体(4年) ・角柱,円柱(5年) ・直方体,立方体も角柱 (5年) ・直方体,立方体の体積 (5年) 1 本時 ・ 三角柱の体積の求め方を考え る。台形の面積の求め方 (上底+下底)×高さ÷2 なので 面積が21㎠の台形 底面の形が変わっても考え方は、同じなので 角柱; まずは、円柱の体積を求めよう! というわけで、まずは円柱の体積を求めます。 底面積 8\times 8\times 314=096 (cm^2) 円柱の体積 096\times 10=096 (cm^3) かず先生 体積を求めたら、それをリットルに変換します!
一部が欠けた横倒し直円柱の半径と高さから体積、側面積、底面積、上面積を計算します。 中空円柱の体積 中空円柱の体積 中空円柱の外半径と内半径と高さから体積、側面積、表面積を計算します。 斜切円柱の体積 斜切円柱の体積考え方や解き方は難しくありませんね! 底面積を求めて、高さをかけるだけ! それでは、円柱の体積問題をバッチリにするため演習問題に挑戦してみましょう! 円柱の演習問題(小学生) 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。
13/8/21 円柱の定義に基づいて 2つの基底の合計面積を求めます。これは、基底が互いに等しいことを示しています。 1つの基本円の面積に2を掛けます、Sky = 2∙Sc = 2∙π∙R²。 3 円柱の側面の表面積を計算します。 これを行うには、 円柱の底の1つを制限する求める面積を S とすると、 上式の定積分の計算は、置換積分を用いてもいいが、軽妙に「四分円の面積」から求め る方が多数だろう。 また、この楕円は、半径 倍縮小して得られるという性質を用い て、 πa 214/1/ 指針(考え方) この円柱の側面積= 2r × 2πr = 4πr2 球の表面積の公式と同じ式をしていることが分かる. あなたは今、 球の表面積を求める公式 を知らないものとします. 円柱の側面積=球の表面積 を示すことによって, (円柱の側面積= 4πr2 なので




円柱の表面積の求め方 側面積の考え方をマスターしよう 中学数学 理科の学習まとめサイト
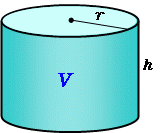



直円柱の体積 高精度計算サイト
円柱の表面積を求める公式は、 S = 2πr^2 2πrh = 2πr(rh) で表されます。 このページでは、例題と共に、円柱の表面積の求め方を説明しています。 お使いのブラウザでは JavaScript が無効になってい13/6/17 円柱の表面積を求めてみよう 具体的に円柱の表面積について考えてみましょう。 この円柱の高さが4㎝、底面の円の半径が3㎝とした場合の表面積の求め方です。 表面積はこの全ての面積を足せばよいので、 9π+9π+24π=42π 答えは42π ㎠になります。11/4/15 円柱の表面積の求め方の公式 をつかってしまえば2秒ぐらいで計算できちゃうんだ。 下の図のように、円柱底面の半径をr、高さをhとすると、 2πr(hr)




丸棒の重量 円柱の体積と重量の求め方 鉄の場合



立体 の 表面積 求め 方
この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める (1) r=5、h29/8/18 円柱の高さ=円柱の体積÷底面積 で求めることができます。 ここで底面積=5×5×314=785 よって、円柱の高さ=628÷785=8(cm)となります。19/2/21 底面の円の面積が \(s_1\)、円柱の側面積が \(s_2\) のとき、円柱の表面積 \(s_s\) は、次の式で求められる。 \begin{align}\color{red}{S_S = 2S_1 S_2}\end{align} (表面積) \(=\) \(2\) (底面積) \(\) (側面積)




角柱 円柱の表面積の求め方 中学数学の柱体の公式と展開図の計算 リョースケ大学




角錐 円錐の体積と表面積の公式 数学fun
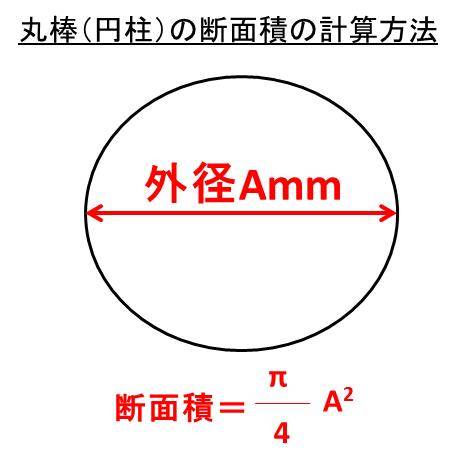
円柱の体積の公式は V=Sh (Sはもちろんπr2) ですので、これらに問題に指定してある円柱の各数値を代入するだけで求められると思います。 問題は円柱の表面積の求め方です。 まず何より表面積と側面積を明確に区別しておく必要があります。 円柱の断面積の求め方 続いて、円柱の鉛直断面積を計算していきましょう。 ・例題2 直径10mm、奥行き15cmの円柱があります。この断面積はいくらと求められるでしょうか。 ・解答2 このとき、円柱の断面(垂直断面)は円になることを活用します。 よって、5 × 5 × 314 = 785mm2が円柱の断面積と計算されました。 円筒(配管)の断面積の求め方角柱の体積の求め方から,円柱の体 積の求積方式を求めることができる。 (1) 生活場面における立体の体積の大き さを,底面や高さを見つけ求め方を説 明することができる。 (1)本時 複合図形の体積の求め方を考えるこ とができる。 (1)




2 を途中式を含めて教えてください Clear



円柱の求め方について なんですが 小学校でやったはずの円柱の体 Yahoo 知恵袋
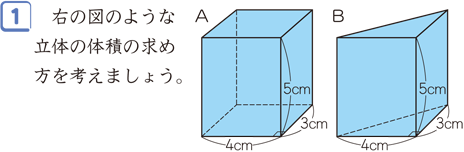
体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方単元名 角柱と円柱の体積の求め方を考えよう ~求積マスターになろう~ 第6学年 男子8名 女子8名 計16名 指導者:長谷川 毅 B 図形(4)立体図形の体積に関わる数学的活動を通して,次の事項を身に付けることができるよう指導する。右図イの四角柱の表面積 底面:3×4=12(cm 2)の長方形が2つ 側面:5×4=(cm 2)の長方形が2つ 側面:5×3=15(cm 2)の長方形が2つ 計94(cm 2)・・・答 図ウの円柱の表面積 ウ 底面: π ×2 2 =4 π (cm 2)の円が2つ 側面:底面の円周の長さと側面の横の長さが等しいから 5×4 π = π (cm 2)の長方



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋
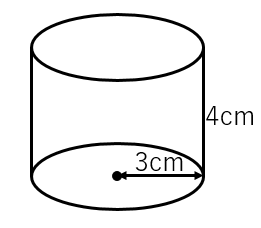



円柱の表面積と体積を求める公式 具体例で学ぶ数学
練習131 球面x 2 y 2 z2 = a の表面積を求めよ。( z = p a ¡x2 ¡y2 の fx2 y2 • a2g 上の曲面積の2倍) 宿題131 1) 二つの円柱x2 y2 • a2, y2 z2 • a2 の共通部分の体積を求 めよ。(変数変換は必要ない) 2) 円柱面x2 y2 = a2, 平面z = 0, 曲面z = x2 y2 で囲まれた領域の体積 を3/2/18 円柱の表面積を求める方法 この円柱を使って解説を行っていきます。 円柱の表面積を求めるためには 底面積と側面積を求めて合計する必要があります。 それでは、底面積と側面積をそれぞれ求めてみましょう。4/3/ 表面積=側面関+底面積+天面積 =156π+36π+36π =228π(cm2) 公式円柱の表面積=底面積×2+側面積 =2×円周率×半径×(高さ半径) =2πr(hr) =2πrh+2πr2練習問題円柱の表面積を計算してみよう




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
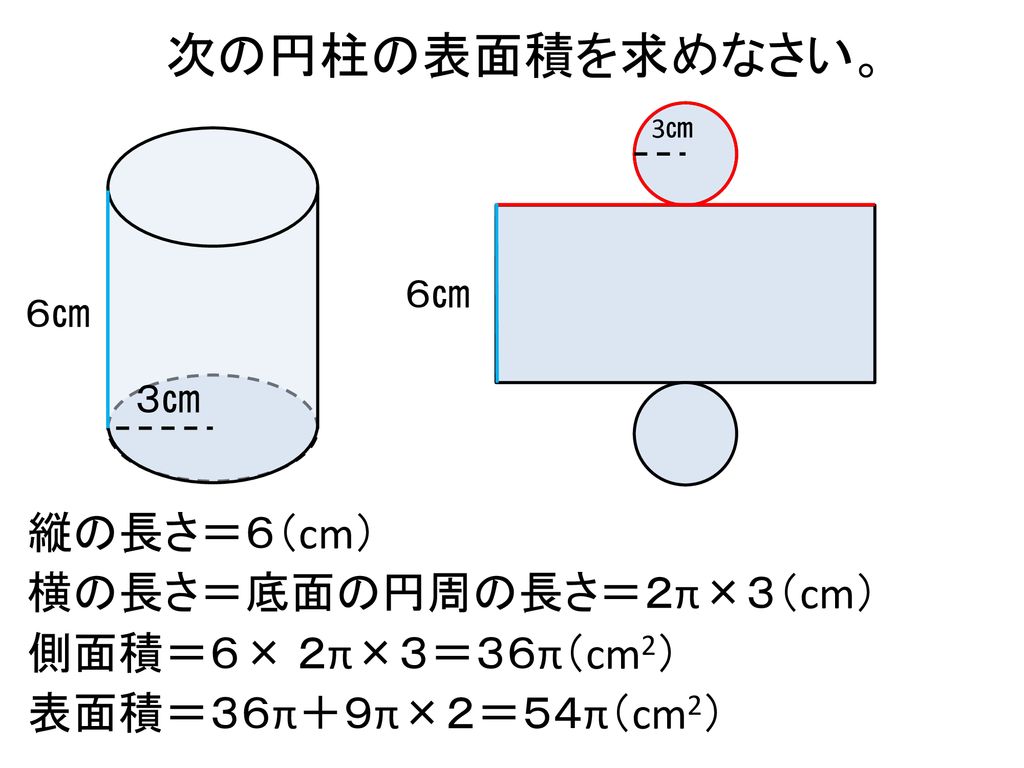



本時の目標 いろいろな立体の表面積を求めることができる Ppt Download




2 の円柱の表面積の求め方を教えてください Clear




円柱の表面積の求め方 公式と計算例
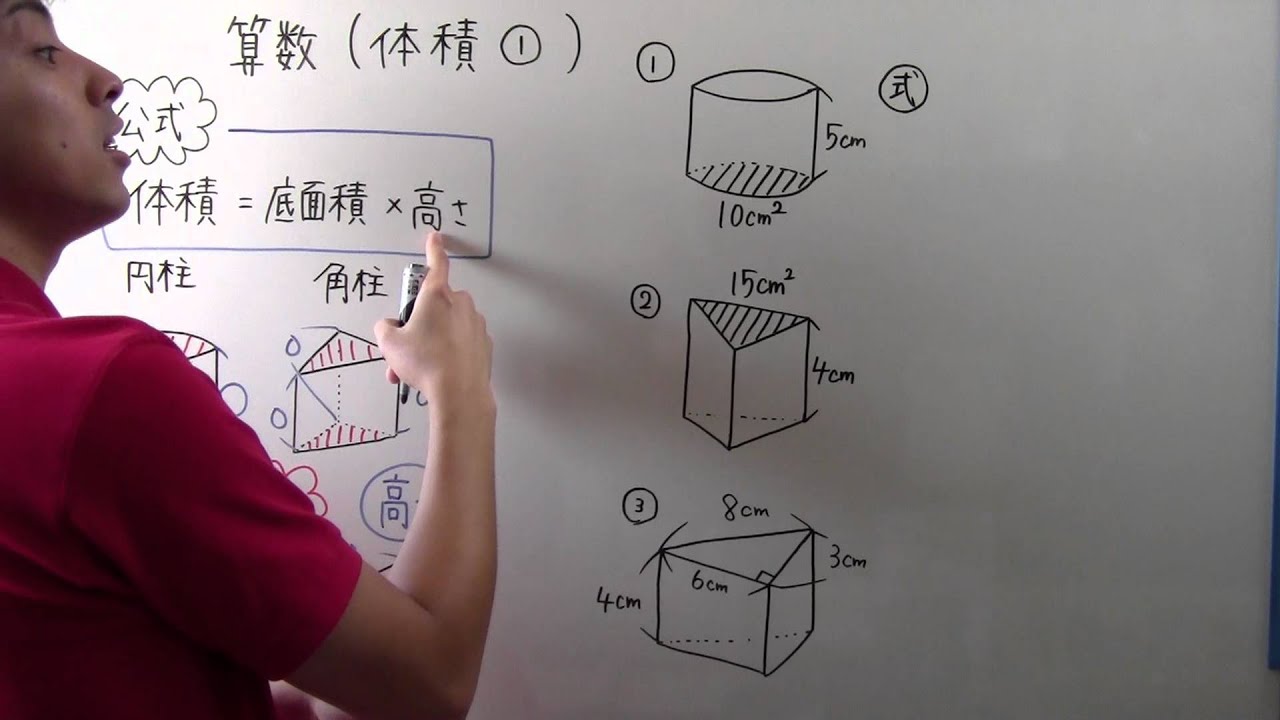



小6 算数 小6 25 体積 円柱 角柱 Youtube
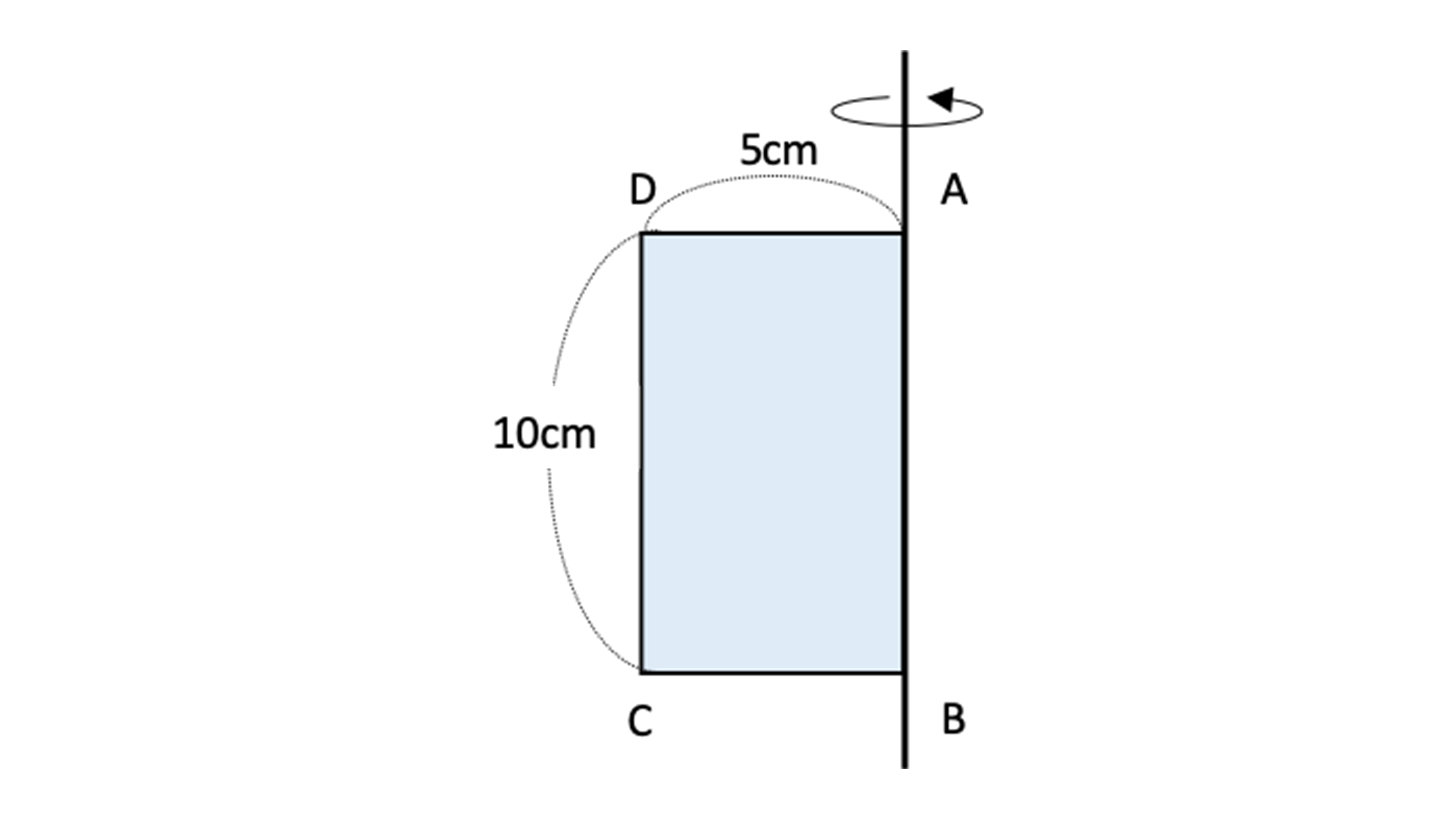



1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円柱の体積の求め方 公式 小学生 中学生の勉強




簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ
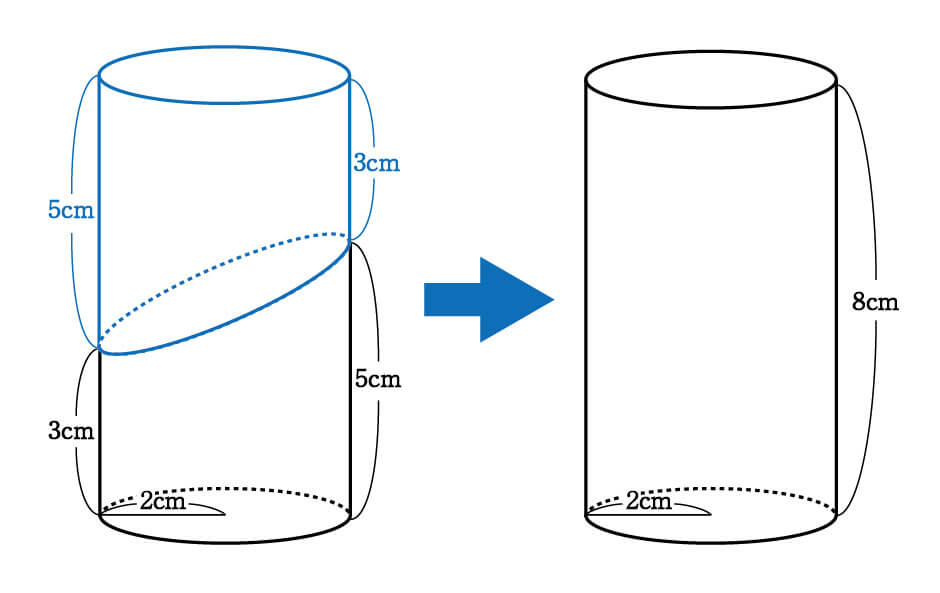



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題




円柱の体積の求め方 公式と計算例




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円柱の表面積の求め方は ちょっと面倒くさいだけ たぬぬ塾 中学校の先生たち



立体の表面積




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
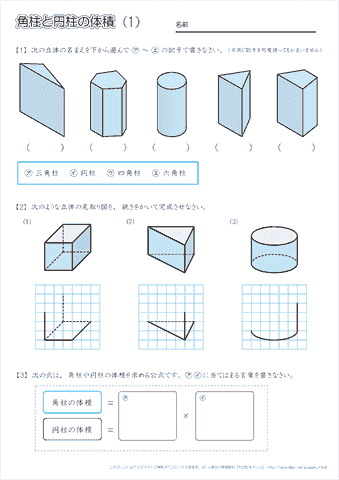



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




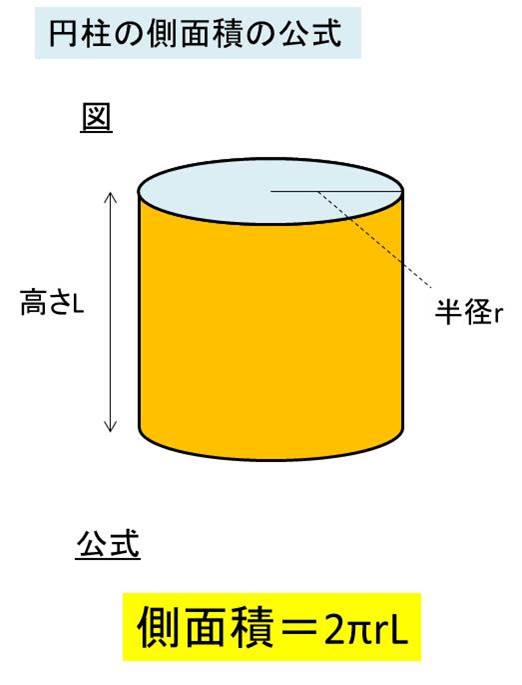
公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




中学1年生 数学 無料問題集 角柱や円柱の体積 おかわりドリル
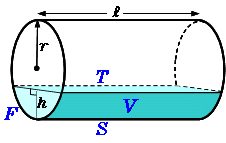



一部が欠けた直円柱の体積 高精度計算サイト




中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




円柱の体積の計算 リットルへの変換も考えてみよう 中学数学 理科の学習まとめサイト




スタディピア 立体の表面積




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




球の表面積と体積の公式 数学fun




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
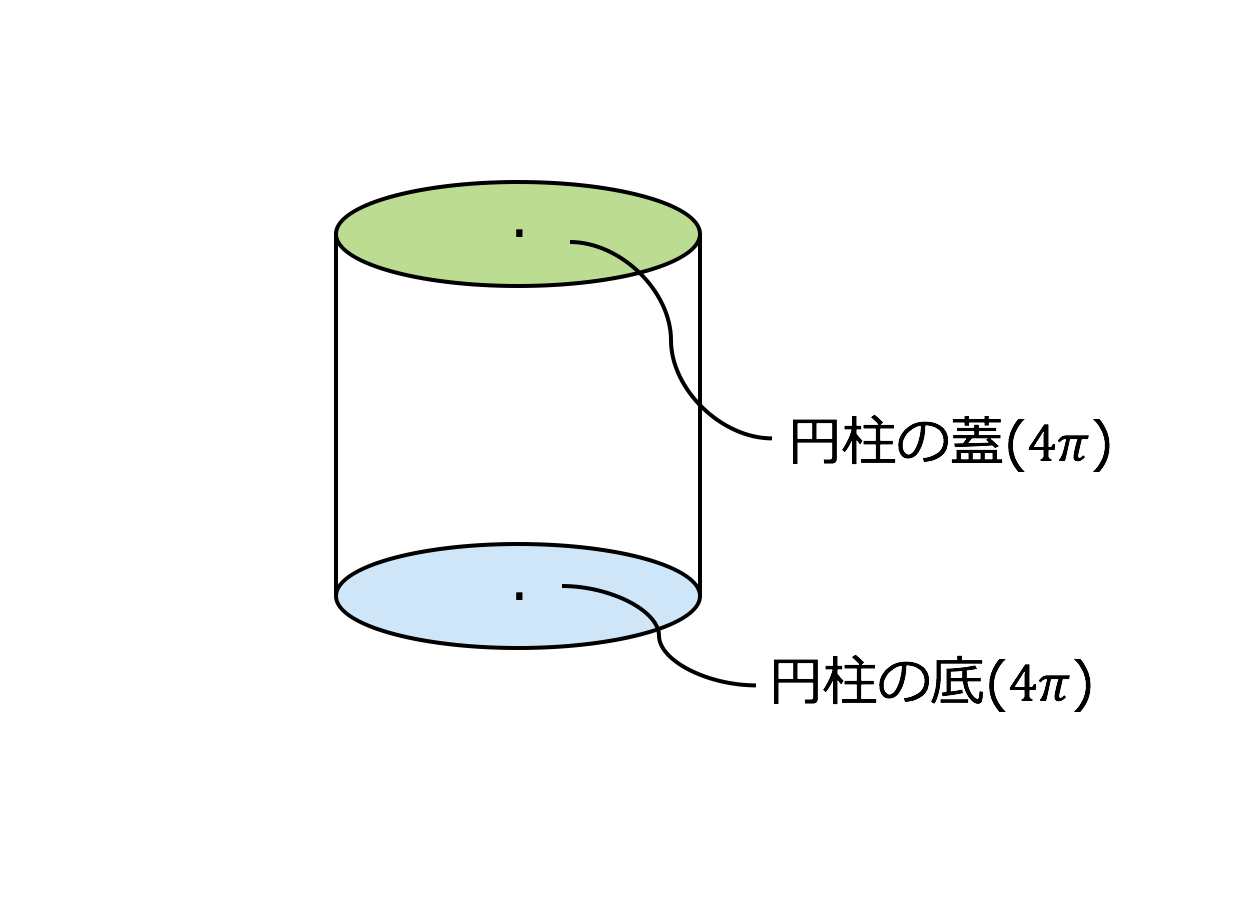



3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




相似な円柱の表面積比 体積比 中学数学 By Okボーイ マナペディア



立体の体積と表面積 1 柱体の表面積




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




角柱 円柱の表面積と体積の公式 数学fun




円柱の表面積の求め方 公式と計算例




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




円柱の表面積 Youtube




円柱の表面積の求め方の基本 現役塾講師のわかりやすい中学数学の解き方




角柱や円柱の表面積の求め方を教えてください Clear
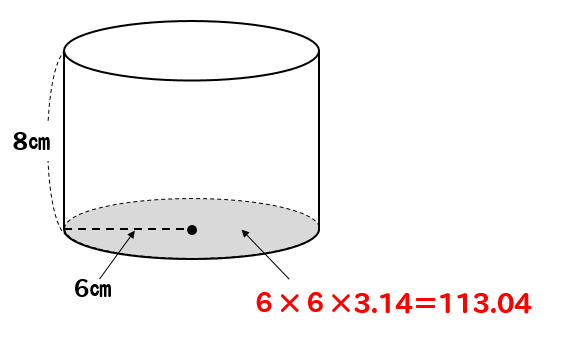



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




円柱の体積の求め方 公式 小学生 中学生の勉強



1




円柱の表面積 Youtube
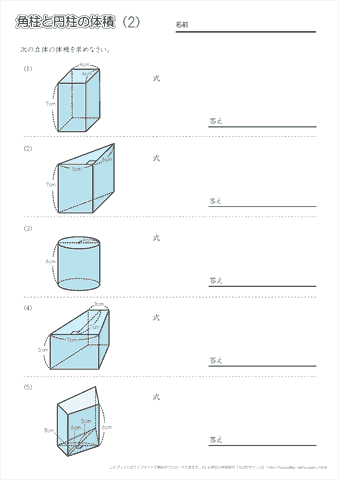



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




円柱の表面積と体積を求める公式 具体例で学ぶ数学
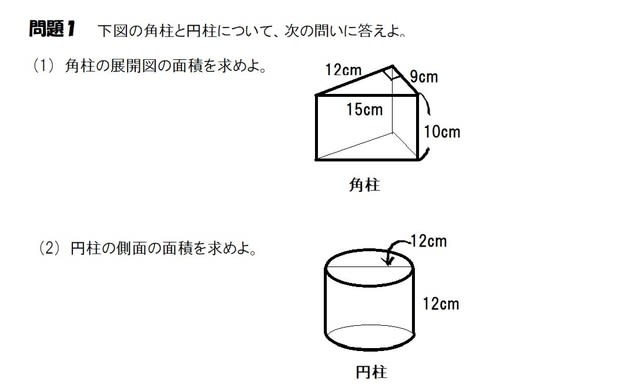



角柱と円柱 展開図を使う 小学5年 算数の教え方教えますmother S Math Happy Study Support




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu
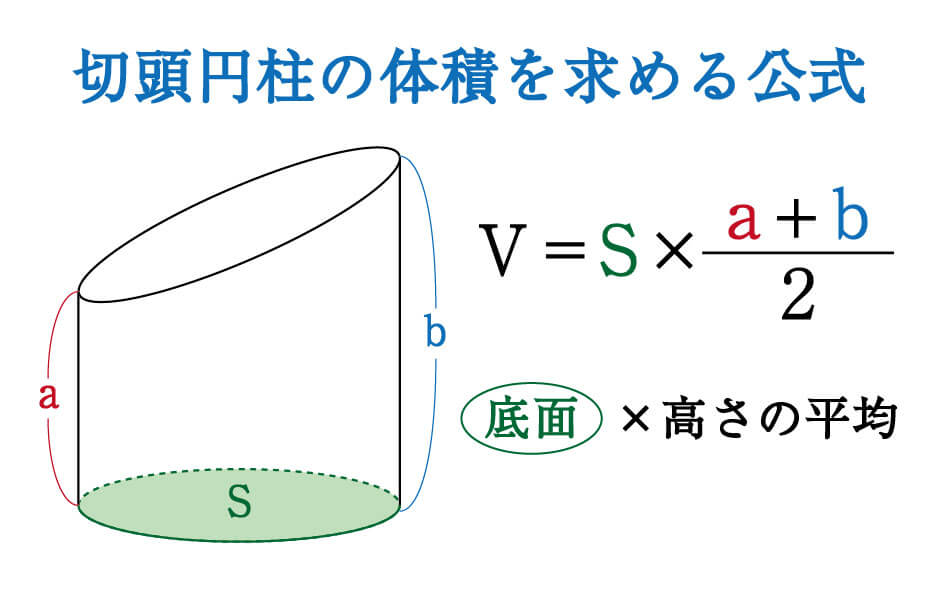



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
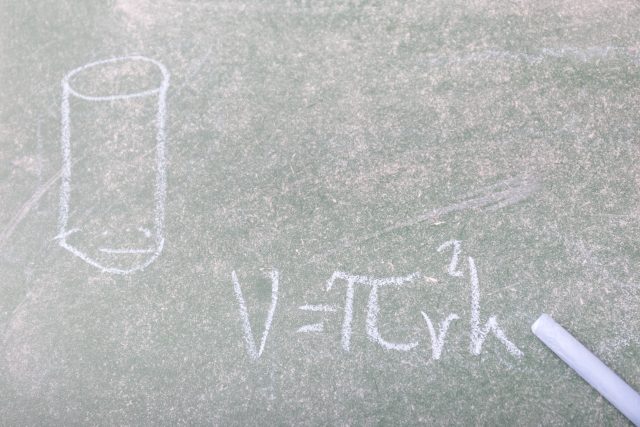



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




表面積の求め方 計算公式一覧



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係
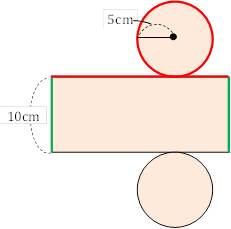



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小6 算数 小6 26 角柱と円柱の体積 基本編 Youtube




円柱の体積の求め方 公式 小学生 中学生の勉強
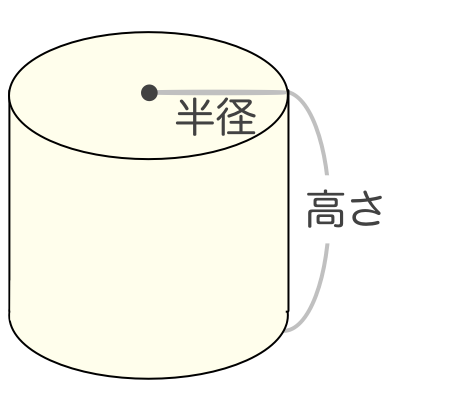



円柱の表面積 簡単に計算できる電卓サイト



3




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
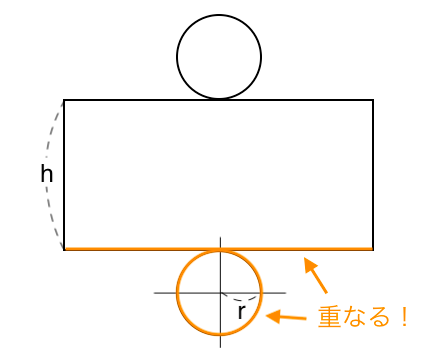



円柱の表面積の求め方 公式にして問題を素早く解く 苦手な数学を簡単に




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円柱の表面積の求め方 公式 小学生 中学生の勉強
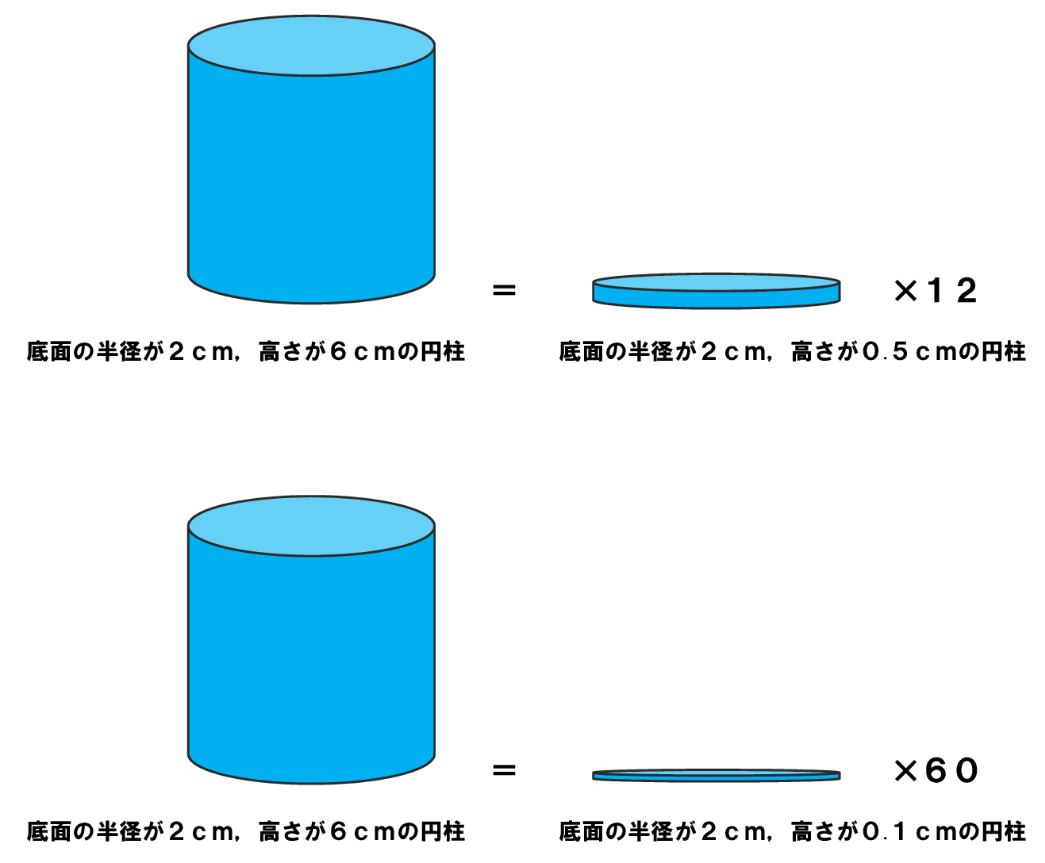



もたこ博士の算数工房 算数から数学まで



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




中1 数学 6 2 角柱 円柱の表面積 Youtube
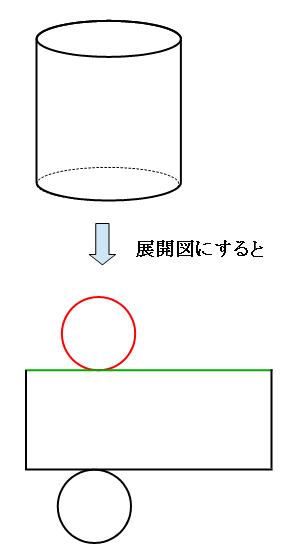



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




円柱の体積と表面積の求め方 展開図とイラストで分かりやすく解説




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾
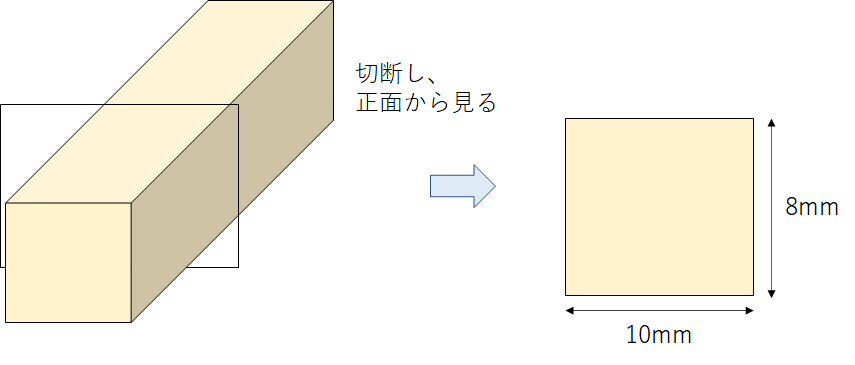



断面積の意味は 四角 長方形 や円筒 配管 や円柱の断面積の計算方法 求め方 は 単位はmm2 水平断面と鉛直断面 垂直断面 ウルトラフリーダム




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



円柱の表面積は 1分でわかる公式 求め方 計算 側面積 底面積との関係



鉄やステンレスの円柱の重量計算 丸棒の重さ 質量 の求め方 白丸くん



1




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ



角柱と円柱の体積 算数用語集




公式不要 円柱の側面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく



円柱の側面積 底面積 表面積を求める方法 白丸くん




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト



5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル



6年算数立体の体積その2 教え方



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典



0 件のコメント:
コメントを投稿