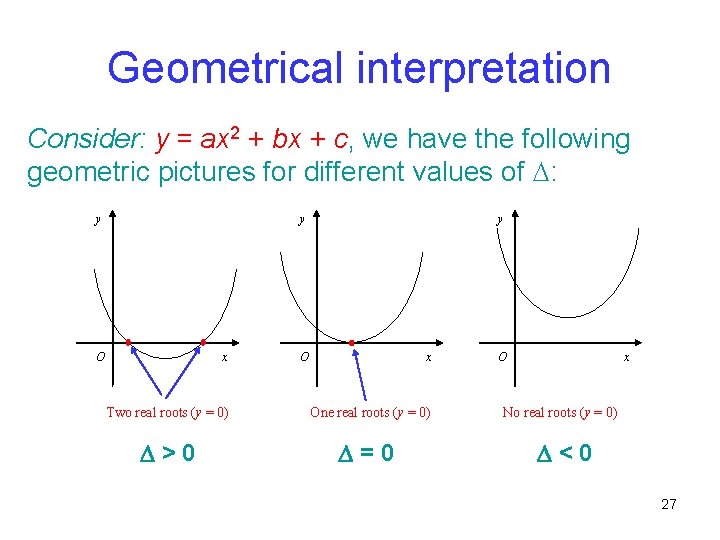
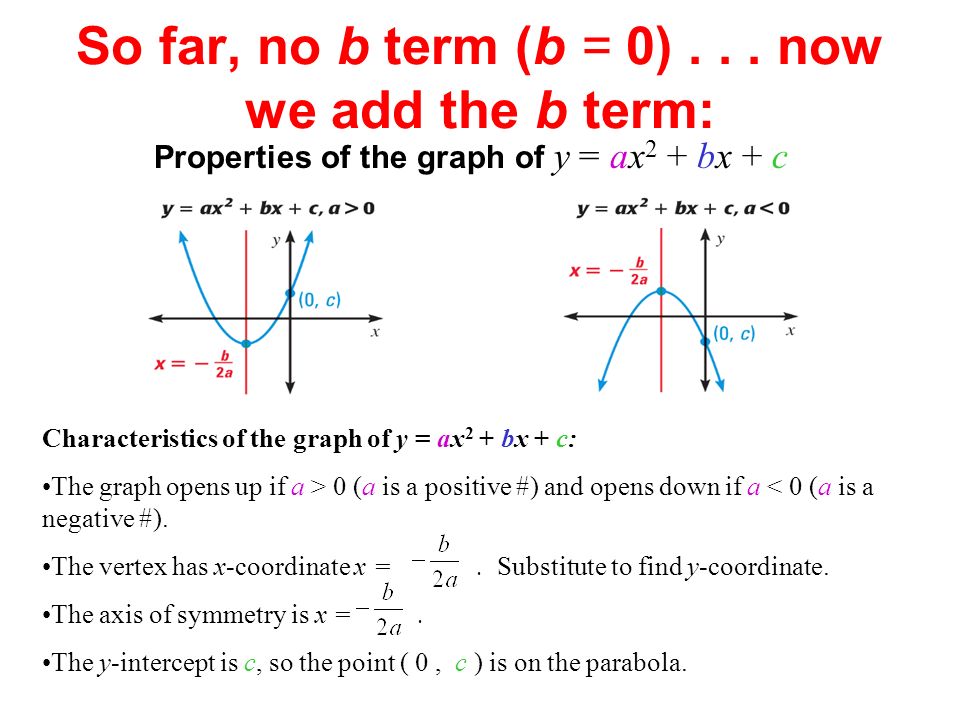
Describe the process with well labeled diagramsThe graph of a quadratic equation in two variables (y = ax2 bx c) is called a parabola The following graphs are two typical parabolas their xintercepts are marked by red dots, their yintercepts are marked by a pink dot, and the vertex of each parabola is marked by a green dot We say that the first parabola opens upwards (is a U shape) and the second parabola opensX 2 4 x !
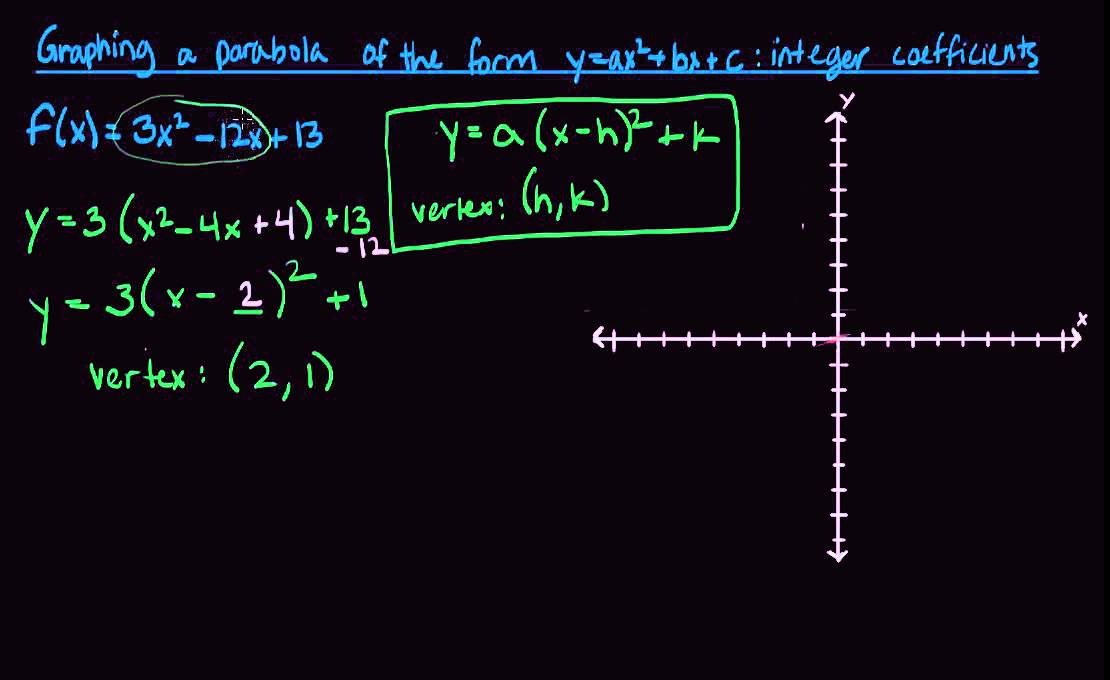
Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube
Y=ax^2 bx c labeled
Y=ax^2 bx c labeled-Set c to 10, the line slopes;C 0 and ax^2bxc has only one solution Answer by KMST(52) (Show Source) You can put this solution on YOUR website!



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
A ≠ 0 then the xcoordinate of the vertex is ∙ xxvertex = − b 2a f (x) = x2 6x 5 is in standard form with a = 1,b = 6 and c = 5 xvertex = − 6 2 = − 3 substitute this value into the equation for ySet d to 25, the line moves up;Exercise #1 Determine the equation of a quadratic function whose roots are —3 and 4 and which passes through the point (2, —50) Express your answer in standard form (y = ax bxc) Verify your answer by
The equation of the tangent at x = 1 has slope 8 and passes through (1 , 0) and its equation is given by y = 8x 8 The equation of the tangent at x = 2 has slope 4 and passes through (2 , 14) and its equation is given by y = 4x 14 c) Graphs of the quadratic function and all1) If there are zeros of 5 and 2, what is the equation of the graph?1) 8 and 0 2) 2 and −4 3) 9 and −1 4) 4 and −2 5 The equation y=ax2 bxc is graphed on the set of axes below Based on the graph, what are the roots of the equation ax2 bxc=0?
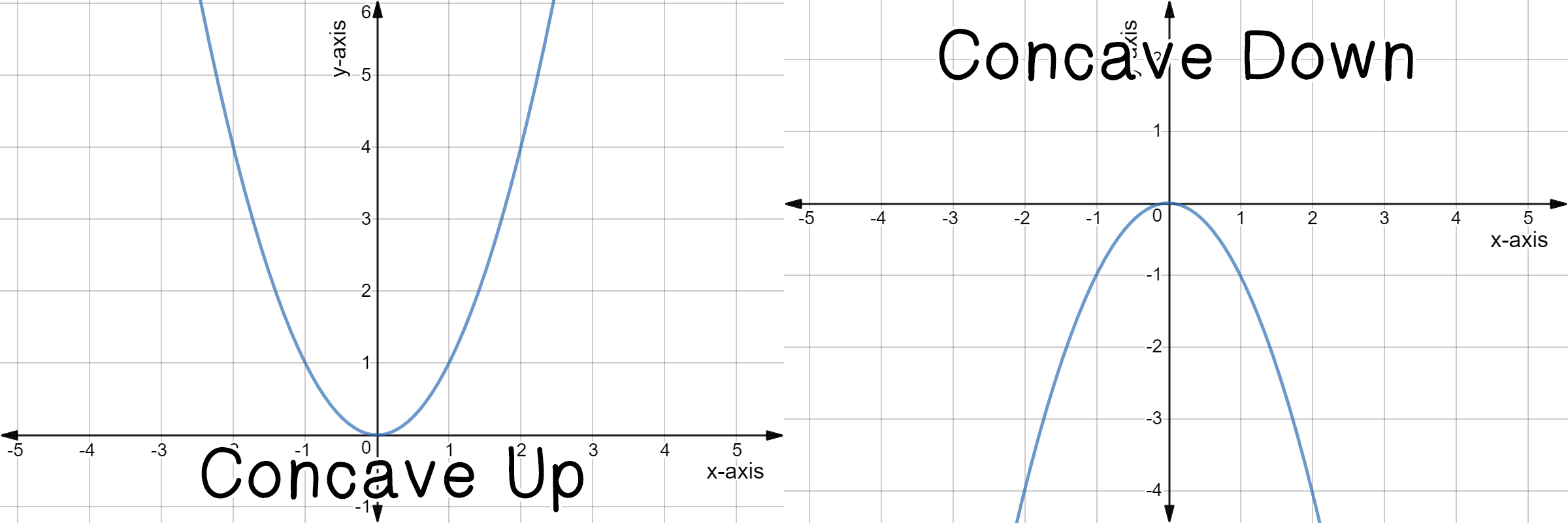
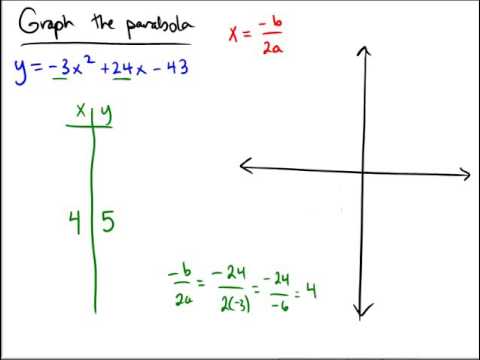
B 2 a You can Þnd the y by plugging x into your equation Example 2 Find the vertex and the axis of symmetry for the following functions a) y =2 x 2 4 x b) y = ! Refer to the explanation The standard form of a parabola is y=ax^2bxc, where a!=0 The vertex is the minimum or maximum point of a parabola If a>0, the vertex is the minimum point and the parabola opens upward If a Explanation given the parabola in standard form ∙ xy = ax2 bx cx;




Task 2 3 5 Flying Through The St Louis Gateway Arch Solutions Pdf Free Download




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions
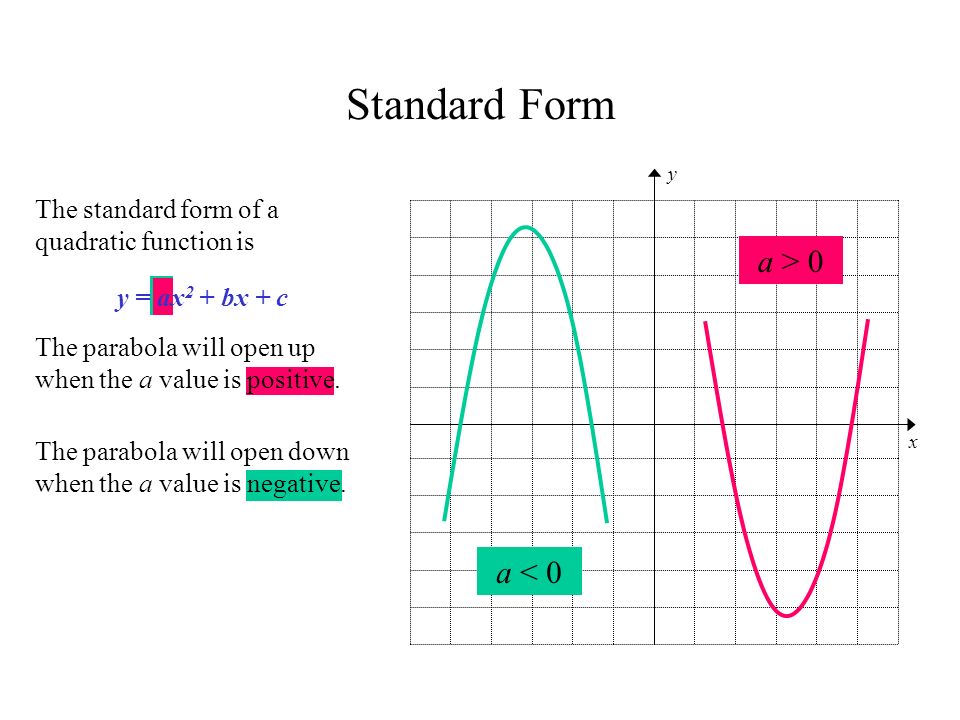
I have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I have The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bxVertex Formula The graph of y = ax 2 bx c has the line x = !



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
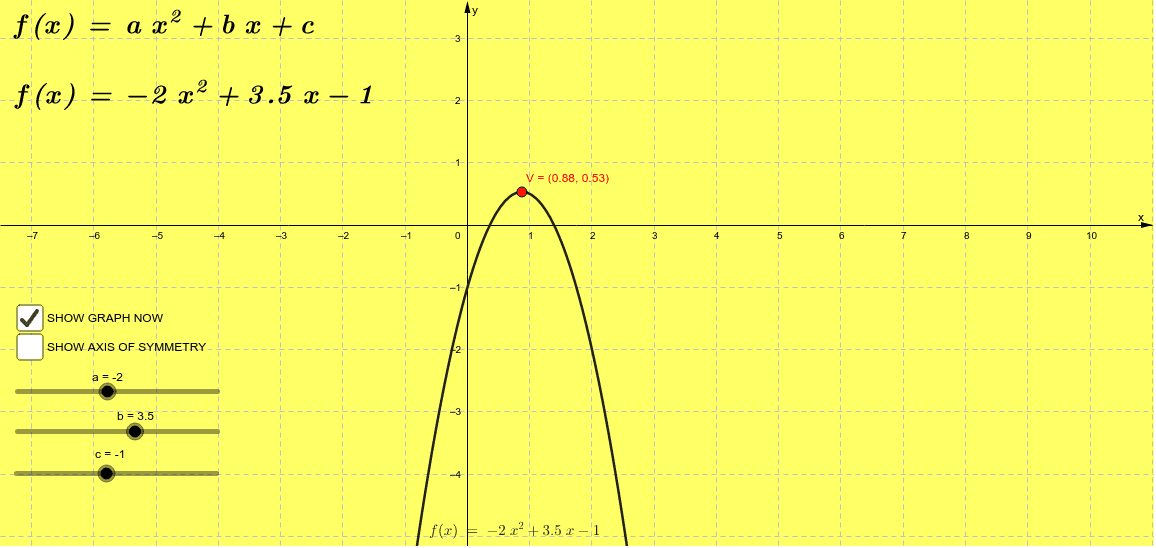



The Quadratic Function Y Ax2 Bx C Geogebra
The model represents a polynomial of the form ax2 bx c An algebra tile configuration 4 tiles are in the Factor 1 spot 3 x , 1 negative 2 tiles are in the Factor 2 spot 1 x, negative 8 tiles are in the Product spot in 4 columns with 2 rowsSuppose we have a parabola y = a x 2 b x c y = ax^2 bx c y = a x 2 b x c Then the equation a x 2 b x c = 0 ax^2 bx c = 0 a x 2 b x c = 0 is bound to have two roots since it is a quadratic equation However, the number of real roots depends on the parabolaWe learn how to find the equation of a parabola by writing it in vertex form In the previous section, we learnt how to write a parabola in its vertex form and saw that a parabola's equation \y = ax^2bxc\ could be rewritten in vertex form \y = a\begin{pmatrix}x h \end{pmatrix}^2k\ where \(h\) is the horizontal coordinate of the vertex



Parabolas




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions
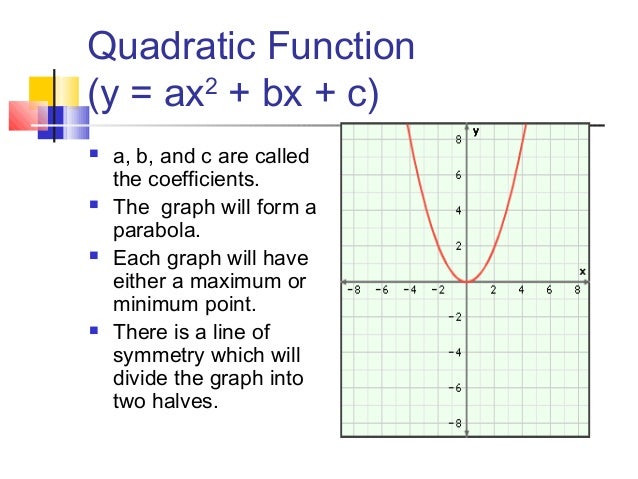
2 marks c 16c2−25=171 a b c=35 x c ±35 6a The graph of the quadratic function intersects the yaxis at point A(0, 5) and has its vertex at point B(2, 9) Write down the value of c f(x)=cbx−x2 2 marks 1 markSet b to 5, The parabola shape is added in Set a to 4 The cubic "s" shape is added in This is the graph of the equation y = 4x 3 5x 225x25 Note how it combines the effects of the four coefficientsAs we spoken in last lesson, quadratic equation is a function whose formula is given in the form of quadratic expression or $ ax^2 bx c = 0$ Where a ≠ 0, b, c are given real numbers Since every function has its own special graph, so does quadratic one Graph of every quadratic equation is a parabola Parabola is a set of points in a



Assignment 2



Graphs Of The Sine And Cosine Function Precalculus Ii
1) 0 and 5 2) 1 andThe graph of a quadratic function is a Ushaped curve called a parabolaOne important feature of the graph is that it has an extreme point, called the vertexIf the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value5 Up/ Down Test The graph of y



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Warm Up Tuesday 8 11 Describe The Transformation Then Graph The Function 1 H X X 9 G X 5x Write The Resulting Equation Ppt Download
B 2 a as its axis of symmetry The x coordinate of the vertex is x = !Ln ax bx c dx a 4ac b2 tan 1 2ax b p 4ac b2 2x b 2a ln ax2 bx c (47) Z xln(ax b)dx= bx 2a 1 4 x2 1 2 x2 b2 a2 ln(ax b) (48) Z xln a2 b2x2 dx= 1 2 x2 1 2 x2 a2 b2 ln a2 b2x2 (49) Integrals with Exponentials ZIf your equation is in the standard form y = a x 2 b x c, then the formula for the axis of symmetry is x = − b 2 a



Quadratics



1
When a 0 in the quadratic function y = ax2 bx C, the graph of the quadratic When a 0 in the quadratic function y = ax2 bx C, the graph of the quadratic function opens _____?Whereas to graph the following equation y equals 5x squared minus x plus 15 so let me get my little scratch pad out so it's y is equal to 5x squared minus x plus 15 now there's many ways to graph this you can just take three values for X and figure out what the corresponding values for Y are just graph those three points and three points actually will determine a parabola but I want toThe quadratic equation itself is (standard form) ax^2 bx c = 0 where a is the coefficient of the x^2 term b is the coefficient of the x term c is the constant term you use the a,b,c terms in the quadratic formula to find the roots the minimum / maximum point of




Regular Algebra 2 Exploring Quadratics Standard Form 21 Minutes Yankton High School



Answered The Graph Of The Function F X Ax2 Bx Bartleby
2) What is the product of (2x 3) and (x 5)?The equation y = ax2 bx c is in factored form when it is written as y = a(xr 1)(xr 2) For the function with equation y = (x 1)(x 4) graphed in Activity 1, a = 1, r 1 = 1, and r 2 = 4 The xintercepts of the function are the values of x for which y = 0 So they are the values of x that satisfy the equation 0 = (x 1)(x 4) Chapter 12 Activity 1 1The solutions of the quadratic equation ax 2 bx c = 0 correspond to the roots of the function f(x) = ax 2 bx c, since they are the values of x for which f(x) = 0 As shown in Figure 2, if a , b , and c are real numbers and the domain of f is the set of real numbers, then the roots of f are exactly the x coordinates of the points where




Prostate Gland Black And The Defined Pz Below Y Ax 2 Bx C Download Scientific Diagram



Mathematics Ability Cheng Kai Ming Department Of Physics
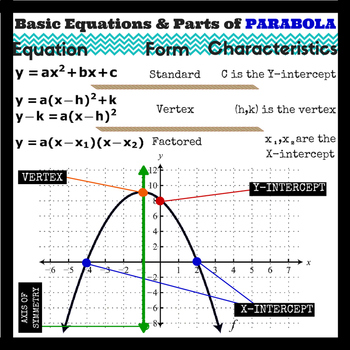
Standard form of a quadratic equation is y=ax 2 bxc, where 'a' is not 0 Vertex form of a quadratic equation is y=a (xh) 2 k, where (h,k) is the vertex of the quadratic function 'a', 'b', and 'c' can be any real number, except 'a' cannot be 0 For our equation, a=1, b=12, and c=32Given a parabola \(y=ax^2bxc\), the point at which it cuts the \(y\)axis is known as the \(y\)intercept The \(y\)intercept will always have coordinates \\begin{pmatrix}0,c\end{pmatrix}\ where \(c\) is the only term in the parabola 's equation without an \(x\)Graphing Quadratic Functions The general form of a quadratic is " y = ax2 bx c " For graphing, the leading coefficient " a " indicates how "fat" or how "skinny" the parabola will be



Assignment 2




Graphing Y Ax2 Bx C Youtube
Another application of quadratic functions is to curve fitting, also called the theory of splines Since a parabola \(\normalsize{y=ax^2bxc}\) is specified by three numbers, it is reasonable to suppose that we could fit a parabola to three points in the plane This isSince y = mx b is an equation of degree one, the quadratic function, y = ax 2 bx c represents the next level of algebraic complexity The parabola also appears in physics as the path described by a ball thrown at an angle to the horizontal (ignoring air resistance)Previous Post Previous Why is mitosis known as equation cell division?




A Parabola With An Equation Of The Form Y Ax 2 Bx C Has The Point 3 1 As Its Vertex If 1 3 Brainly Com




Y Ax2 Bx C Quadratic Function Ppt Download
The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y y axis The coefficients a,b, a, b, and c c in the equation y =ax2 bxc y = a x 2 b x c control various facets of what the parabola looks like when graphedQuadratic function has the form $ f(x) = ax^2 bx c $ where a, b and c are numbers You can sketch quadratic function in 4 steps I will explain these steps in following examples Example 1 Sketch the graph of the quadratic function $$ {\color{blue}{ f(x) = x^22x3 }} $$ Solution In this case we have $ a=1, b=2 $ and $c=3$Key Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;



1




Refer The Picture Also Y Ax 2 Bx C Hd Png Download Transparent Png Image Pngitem
58 Chapter 2 Quadratic Functions Finding Maximum and Minimum Values Because the vertex is the highest or lowest point on a parabola, its ycoordinate is the maximum value or minimum value of the function The vertex lies on the axis of symmetry, so the function is increasing on one side of the axis of symmetry and decreasing on the other side CCore ore CConceptonceptIf the graph of the quadratic function \(y = ax^2 bx c \) crosses the xaxis, the values of \(x\) at the crossing points are the roots or solutions of the equation \(ax^2 bx c = 0 \) If The graph of the equation y =ax^2 bx c, where a, b, and c are constants, is Geometrically speaking, a parabola is defined as the set of points that are the same distance from a given point and a given line



The Basic Characteristics Of Quadratic Functions Studypug



Quadratic Graph Example Y Ax C Expii
2 y2 = 4x 2 y3 = 2 1 x2 y4 = 10x 2 y5 = –4x 2 y6 = 25x 2 y7 = –0,5x 2 2 Describe the effect of a change in a on the graph of y = ax2 3 Make a table of y1 , y2 , y3 , y4 , for values of x from –3 to 3, or use the TABLE facility of the graphing calculator Describe patterns in the values of y1 Describe patterns in the values of y2 Step 1, Accept a parabola in standard formula format, ie y = ax^2 bx cStep 2, Find the following elements, which you also memorize the methods or formulas for per the following KEY Determine whether element a of the equation is positive and the parabola has a minimum and opens up, or a is negative, and the parabola has a maximum and opens down Find the Axis ofThe full cubic (y = ax 3 bx 2 cxd) Click 'zero' on all four sliders;



Intro To Quadratic Graphs Key Features Of Parabolas Expii



Hq Parabola Equations Graphing Classroom Poster X Tpt
\f(x)=ax^2bxc \\ f(x)=2x^2−6x7\ Using the vertex to determine the shifts, \f(x)=2\Big(x–\dfrac{3}{2}\Big)^2\dfrac{5}{2}\ Analysis One reason we may want to identify the vertex of the parabola is that this point will inform us what the maximum or minimum value of the function is, \((k)\),and where it occurs, \((h)\) The trinomial form ax2 bx c is a quadratic form We need to bring in zero pairs because we need to get the roots of that quadratic equation The roots is referred to as the solutions or the possible value of x to make the equation true jd3sp4o0y and 503 more users found this answer helpful heart outlinedYou mean that has only one solution




The Diagram Shows The Graph Of Y Ax 2 Bx C Then




Task 2 3 5 Flying Through The St Louis Gateway Arch Solutions Pdf Free Download
$ y = ax^2 bx c $ The role of a in $$ \color{Red}{a}x^2 bx c $$ $$ a > 0 $$ parabola's opens upwards like a 'U' $$ a < 0 $$ parabolas opens downwards like an upside down 'U' If $$a < 1 $$, the graph of the parabola's widens This just means that the "U" shape of parabola stretches out sideways4 The equation y=−x2 −2x8 is graphed on the set of axes below Based on this graph, what are the roots of the equation −x2 −2x8 =0?When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if a



Parabolas



Exploring Y Asin Bx C D
Flood hazard areas identified on the Flood Insurance Rate Map are identified as a Special Flood Hazard Area (SFHA) SFHA are defined as the area that will be inundated by the flood event having a 1percent chance of being equaled or exceeded in any given year The 1percent annual chance flood is also referred to as the base flood or 100year flood SFHAs are labeled asQuestion Mat Lab Problem Create Plots Of The Following Functions From X=0 To 10 (a) Y=e^x (b) Y=sin(x) (c) Y=ax^2bxc,where A=5,b=2,c=4 (d) Y=x^1/2 Combine These Into One Figure With Four Sub Windows Using Subplot Function Of Matlab Each Of Your Plots Should Include A Title An Xaxis ,a Yaxis Label And GridSuppose you have ax 2 bx c = y, and you are told to plug zero in for yThe corresponding xvalues are the xintercepts of the graph So solving ax 2 bx c = 0 for x means, among other things, that you are trying to find xinterceptsSince there were two solutions for x 2 3x – 4 = 0, there must then be two xintercepts on the graphGraphing, we get the curve below



Quadratics




Match The Appropriate Form Of The Particular Solution Chegg Com
Every quadratic has a (single) yintercept The reason for this is that the yintercept is the function value at x = 0, and we can always substitute x = 0 into the quadratic Thus, the yintercept of the quadratic function y = ax 2 bx c is c For the other forms of the function, just substitute x = 0 to find the corresponding value of yIt would be nice to be able to fit the curve, specifically through the origin (y=Ax^2Bx regression) 2 0604 Under years old / Highschool/ University/ Grad student / Very / Purpose of use showed me a step by step way to do quadratic regression equationsQuestion Can you please help me to sketch the graph, given is y=ax^2bxc where a 0 ;




The Equation Ax2 Bx C 0 Has No Real Solutions Which Statement About The Graph Of F X Ax2 Brainly Com




Graphing Parabolas
So, given a quadratic function, y = ax 2 bx c, when "a" is positive, the parabola opens upward and the vertex is the minimum value On the other hand, if "a" is negative, the graph opens downward and the vertex is the maximum value
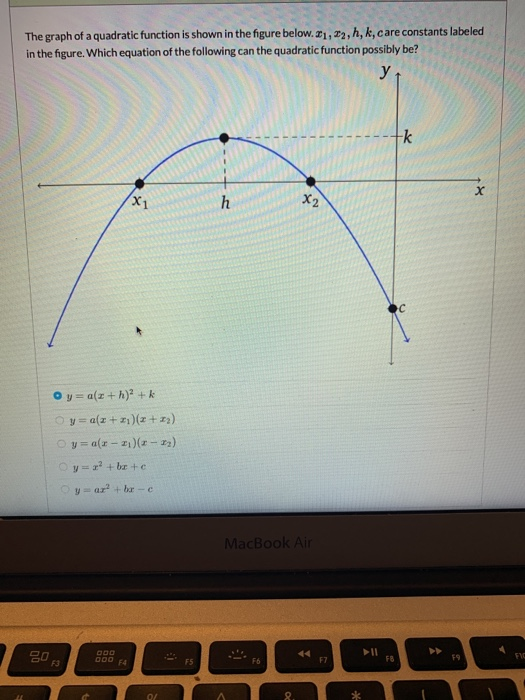



The Graph Of A Quadratic Function Is Shown In The Chegg Com




Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download
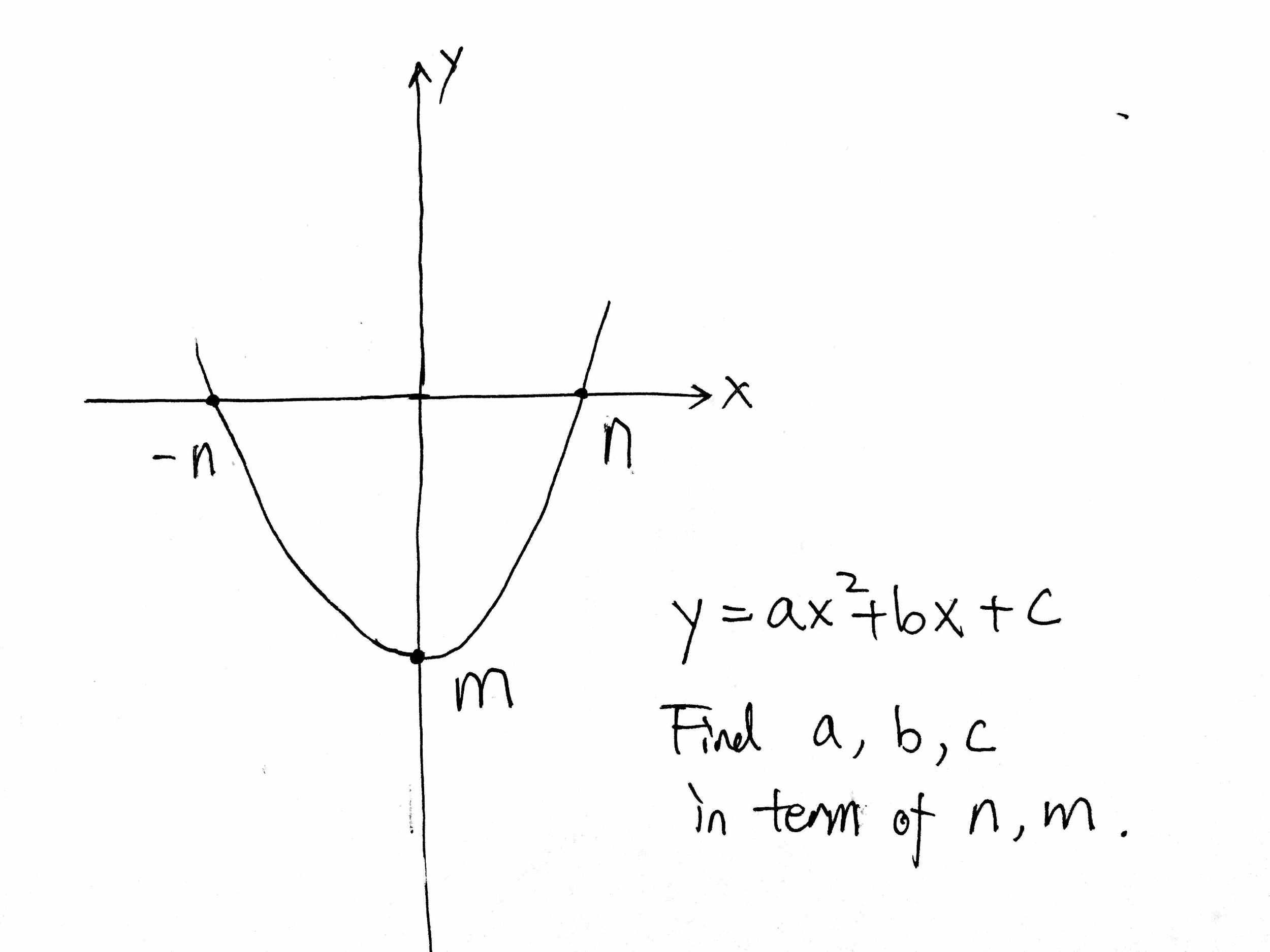



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com



Exploring Parabolas Y Ax 2 Bx C
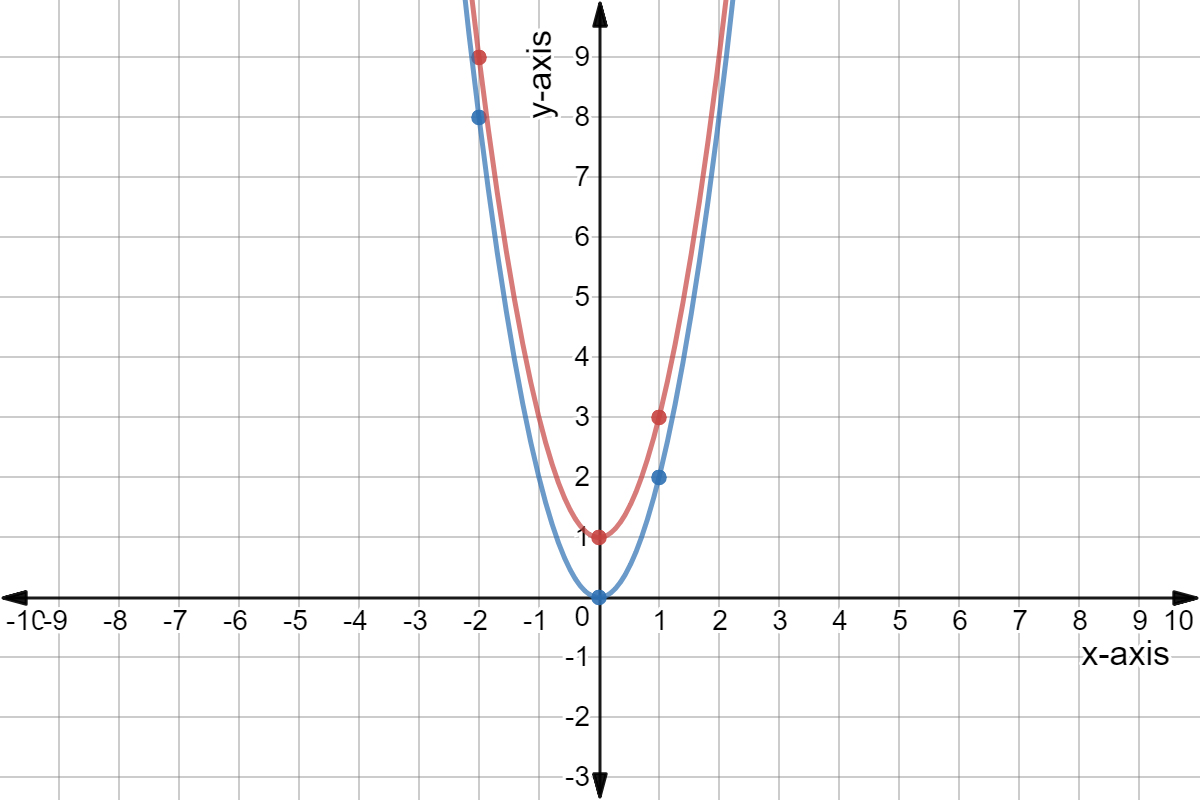



Quadratic Graph Example Y Ax C Expii
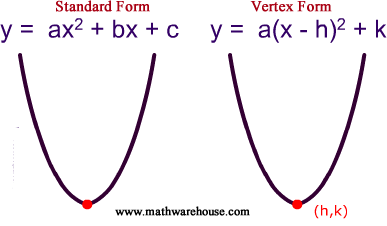



Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph




Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download




The Graph Of Y Ax2 Bx C In The Standard X Y Coordinate Plane Act Math Exam Questions With Answers




Quadratic Graph Example Y Ax Expii




For All Functions Of The Form F X Ax 2 Bx C Which Is True When B 0 Brainly Com



2



Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download



Graphing Quadratic Functions In Standard Form Y Ax 2 Bx C Ppt Download




Pin On Algebra Ii



5 1 Quadratic Functions




The Graph Of Y Ax 2 Bx C Youtube




Solve Quadratic Inequalities Intermediate Algebra



Unique Quadratic Equation In The Form Y Ax 2 Bx C




Graphing Quadratics Standard Form And Vertex Form Posters Reference Sheet Graphing Quadratics Quadratics Quadratic Functions




Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Assignment Pencil Red Pen Highlighter Textbook Gp Notebook



Exploring Parabolas Y Ax 2 Bx C



2
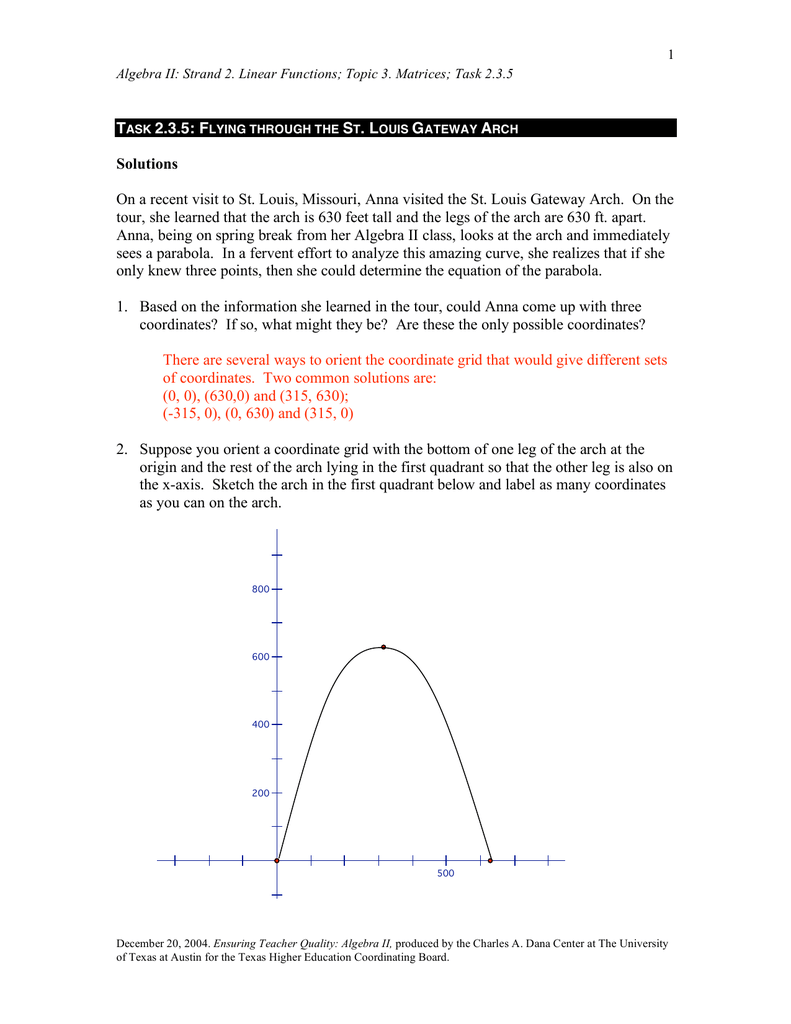



On A Recent Visit To St Louis Missouri Anna Visited Tour She Learned That The Arch Is 630 Feet Tall T
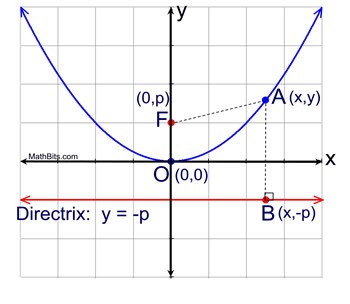



Parabola Equations Mathbitsnotebook Geo Ccss Math
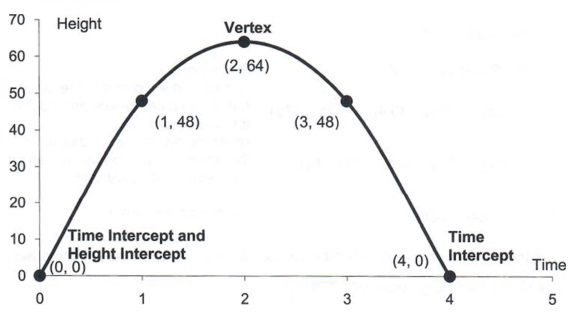



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



Parabolas



Static Bigideasmath Com Protected Content Pe Hs Sections Alg2 Pe 03 04 Pdf




Ppt Vertex Form Powerpoint Presentation Free Download Id



Math Spoken Here About Quadratics 3




Quadratic Function
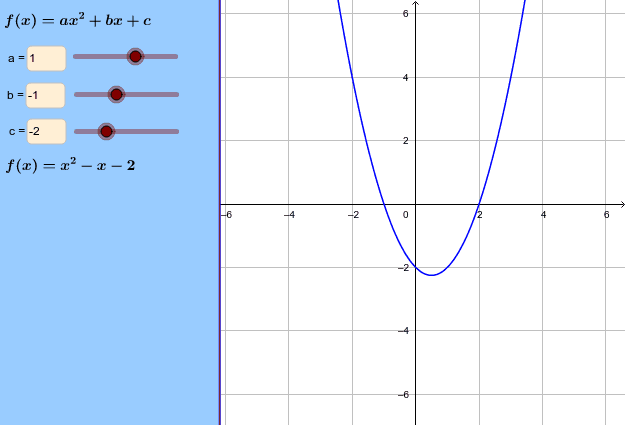



The Graph Of Y Ax 2 Bx C Geogebra




Finding The Parts Of A Parabola Ck 12 Foundation
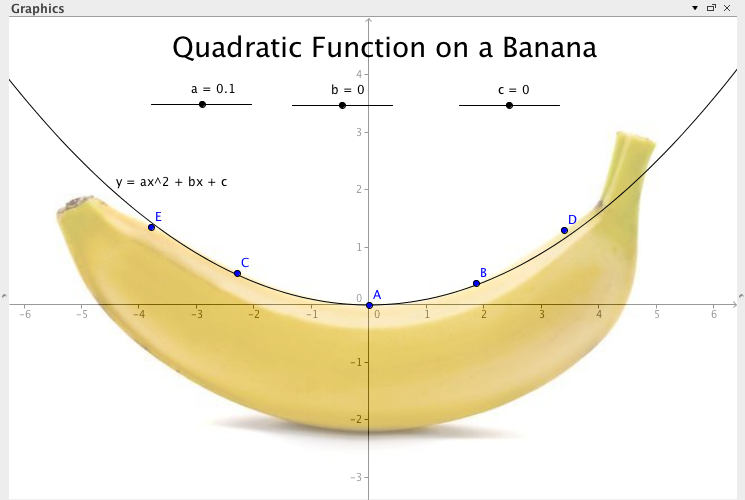



Quadratic Function
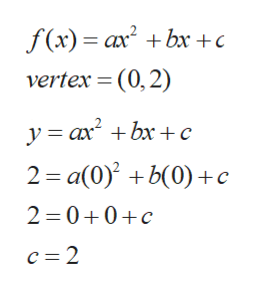



Answered The Graph Of The Function F X Ax2 Bx Bartleby
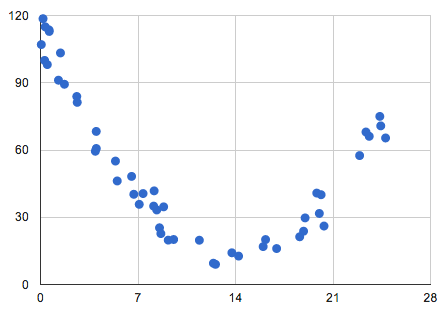



Quadratic Regression Simple Definition Ti Calculator Instructions Statistics How To
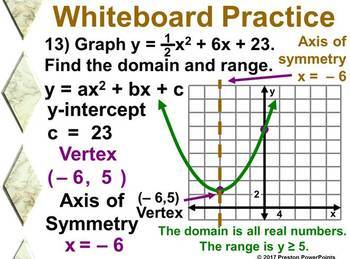



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt




Graphing Y Ax 2 Bx C




Graphing Y Ax 2 Bx C




Interactive Parabola Animation Learnist Quadratics Functions Algebra Parabola



Quadratic Functions




Prostate Gland Red And The Defined Pz Below Y Ax 2 Bx C Green Download Scientific Diagram




Factor And Solve Quadratic Equations Ppt Video Online Download



Quadratic Functions




Finding The Parts Of A Parabola Ck 12 Foundation



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau
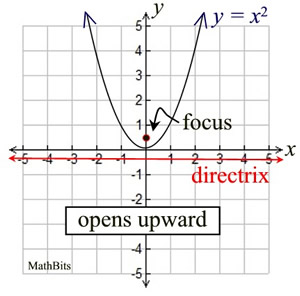



Parabola Equations Mathbitsnotebook Geo Ccss Math
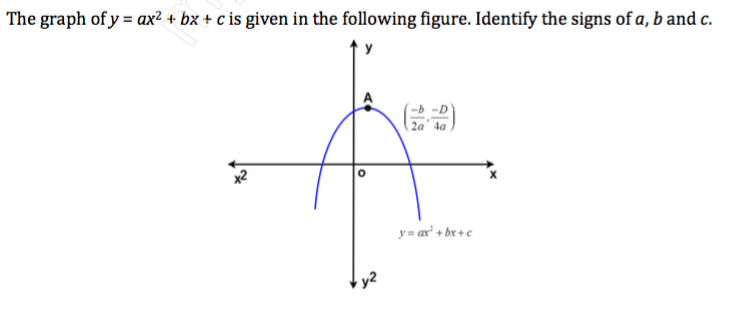



The Graph Of Y Ax 2 Bx C Is Given In The Chegg Com



Equation Of A Line Y Mx B Equation Of A Parabola Y Ax2 Bx C Quadratic Equation Y Ax3 Bx2 Cx D F



Www Cgsd Org Site Handlers Filedownload Ashx Moduleinstanceid 280 Dataid 1436 Filename 408 Smp Seaa C06l06 Pdf




Mfg Graphing Parabolas




Prostate Gland Red And The Defined Pz Below Y Ax 2 Bx C Green Download Scientific Diagram




View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A



Www K12northstar Org Cms Lib Ak Centricity Domain 4806 Alg1 quadratics packet blank Pdf




Help Please For A Quadratic Equation Of The Form 0 Ax2 Bx C To Have Two Zeros What Must Be Brainly Com



Three Parabolas



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 p2 unit 2 2 note packet lg 1019 complete lt 8 to end Pdf



Education Ti Com Media 8bf5fea4b26bfcaf0




Graphing Quadratic Functions In Vertex Standard Form Axis Of Symmetry Word Problems Youtube



1



Math Spoken Here About Quadratics 3



2




Use The Graph Of Y Ax2 Bx C To Solve A Chegg Com




Quadratic Function



Additional Vocabulary Support Manualzz



Unique Quadratic Equation In The Form Y Ax 2 Bx C
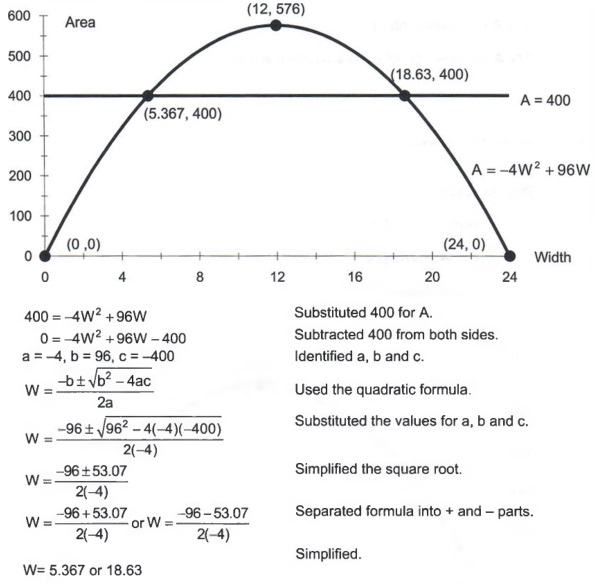



Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube



0 件のコメント:
コメントを投稿